DYLEMAT - geometria analityczna
Cinu:
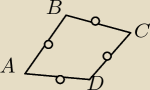
Oblicz obwód czworokąta , którzy OTRZYMAMY łącząc środki boków czworokąta ABCD, jeżeli
A= (−3, −2) B= (−1, 2) C= (3,0) D= (1,−2)
o − na rysunku oznacza srodek np. AB itd...
ABCD − wierzchołki
ŚRODEK BOKÓW
|AB| = (2,0) ŚR A
|BC| = (1,1) B
|CD| = (2,−1) C
|AD| = (−1,−2) D
Wiecie o co chodzi

ODLEGŁOŚCI BOKÓW
|AB| =
√10
|AC| =
√5
|BC|=
√5
|CD| =
√10
Objętość = 2(
√5+
√10)
Dlaczego nie muszę tutaj obliczać długości np. |A+D| |A+C| − spójrz z środkowych czworokąta

nie z DLUGOŚCI




Eta:
środek boku AB −−−− S
1(
−2,0)
" " BC −−−− S
2(1,1)
" " CD −−−− S
3(2,−1)
" " AD −−−− S
4(−1,−2)
boki tego nowego czworokąta S
1S
2S
3S
4
to |S
1S
2| =
√10
|S
2S
3|=
√5
|S
3S
4|=
√10
|S
4S
1|=
√5
to Ob(S
1S
2S
3S
4)= 2(
√5+
√10) [ j ]
więc nie bardzo wiem o co Ci chodzi

 Oblicz obwód czworokąta , którzy OTRZYMAMY łącząc środki boków czworokąta ABCD, jeżeli
A= (−3, −2) B= (−1, 2) C= (3,0) D= (1,−2)
o − na rysunku oznacza srodek np. AB itd...
ABCD − wierzchołki
ŚRODEK BOKÓW
|AB| = (2,0) ŚR A
|BC| = (1,1) B
|CD| = (2,−1) C
|AD| = (−1,−2) D
Wiecie o co chodzi
Oblicz obwód czworokąta , którzy OTRZYMAMY łącząc środki boków czworokąta ABCD, jeżeli
A= (−3, −2) B= (−1, 2) C= (3,0) D= (1,−2)
o − na rysunku oznacza srodek np. AB itd...
ABCD − wierzchołki
ŚRODEK BOKÓW
|AB| = (2,0) ŚR A
|BC| = (1,1) B
|CD| = (2,−1) C
|AD| = (−1,−2) D
Wiecie o co chodzi ODLEGŁOŚCI BOKÓW
|AB| = √10
|AC| = √5
|BC|= √5
|CD| = √10
Objętość = 2(√5+√10)
Dlaczego nie muszę tutaj obliczać długości np. |A+D| |A+C| − spójrz z środkowych czworokąta
ODLEGŁOŚCI BOKÓW
|AB| = √10
|AC| = √5
|BC|= √5
|CD| = √10
Objętość = 2(√5+√10)
Dlaczego nie muszę tutaj obliczać długości np. |A+D| |A+C| − spójrz z środkowych czworokąta nie z DLUGOŚCI
nie z DLUGOŚCI



